Talesystemer og vilkår

Tre hovedområder av forskjell fra våre tall

Tenk hvor mye lettere det ville være å lære seg aritmetikk de første årene hvis alt du måtte gjøre var å lære å skrive en linje som jeg og en trekant. Det er i utgangspunktet alt de eldgamle menneskene i Mesopotamia måtte gjøre, selv om de varierte dem hit og dit, langstrakte, snu osv.

De hadde ikke våre penner og blyanter, eller papir for den saks skyld. Det de skrev med var et verktøy man ville bruke i skulptur, siden mediet var leire. Enten dette er vanskeligere eller enklere å lære å håndtere enn en blyant er en kaste opp, men så langt er de foran i leteavdelingen, med bare to grunnleggende symboler å lære.

Neste trinn kaster en skiftenøkkel inn i enkelhetsavdelingen. Vi bruker a Base 10, et konsept som virker åpenbart siden vi har 10 sifre. Vi har faktisk 20, men la oss anta at vi bruker sandaler med beskyttende tåbelegg for å holde av sanden ørkenen, varm fra den samme solen som ville bake leiretabletter og bevare dem for å finne tusenår seinere. Babylonierne brukte denne Base 10, men bare delvis. Til dels brukte de Base 60, det samme tallet vi ser rundt oss på minutter, sekunder og grader av en trekant eller sirkel. De var dyktige astronomer, og antallet kunne komme fra observasjonene av himmelen. Base 60 har også forskjellige nyttige faktorer i seg som gjør det enkelt å beregne med. Fortsatt er det å måtte lære Base 60 skremmende.

I "Hyllest til Babylonia" [The Mathematical Gazette, Vol. 76, nr. 475, "The Use of the Mathematics History in the Teaching of Mathematics" (Mar., 1992), s. 158-178], forteller forfatterlærer Nick Mackinnon at han bruker babylonsk matematikk for å lære 13-åringer om andre baser enn 10. Det babylonske systemet bruker base-60, noe som betyr at i stedet for å være desimal, er det sexagesimal.

Både det babylonske tallsystemet og vårt er avhengige av posisjon til å gi verdi. De to systemene gjør det annerledes, delvis fordi systemet deres manglet null. Å lære det babyloniske venstre til høyre (høye til lave) posisjonssystemet for en første smak av grunnleggende aritmetikk, er sannsynligvis ikke mer vanskelig enn å lære oss den to-retningsbestemte, der vi må huske rekkefølgen på desimaltallene - øker fra desimalen, en, titalls, hundrevis, og deretter vende ut i den andre retningen på den andre siden, ingen andre kolonne, bare tideler, hundrelapper, tusendeler osv.

Jeg vil gå inn i stillingene til det babylonske systemet på flere sider, men først er det noen viktige tallord å lære.

Vi snakker om perioder med år som bruker desimalmengder. Vi har et tiår i 10 år, et århundre i 100 år (10 tiår) eller 10X10 = 10 år i kvadrat, og et årtusen i 1000 år (10 århundrer) eller 10X100 = 10 år i kubikk. Jeg vet ikke om noe høyere begrep enn det, men det er ikke enhetene babylonerne brukte. Nick Mackinnon viser til et nettbrett fra Senkareh (Larsa) fra Sir Henry Rawlinson (1810-1895) * for enhetene babylonerne brukte og ikke bare for årene det gjaldt, men også antydede mengder:

1. Soss
2. ner
3. sar.

sossnersosssarsoss

Fortsatt ingen bindingsbryter: Det er ikke nødvendigvis enklere å lære kvadratiske og kubiske årsvinkler fra latin enn det er en stavelse babylonske som ikke involverer kubing, men multiplikasjon med 10.

Hva tror du? Hadde det vært vanskeligere å lære antall grunnleggende som babylonisk skolebarn eller som en moderne student på en engelsktalende skole?

* George Rawlinson (1812-1902), Henrys bror, viser et forenklet transkribert tabell med firkanter De syv store monarkiene i den gamle østlige verden. Tabellen ser ut til å være astronomisk, basert på kategoriene i babyloniske år.

Alle bilder kommer fra denne online skannede versjonen av en utgave fra 1800-tallet av George Rawlinson De syv store monarkiene fra den gamle østlige verden.

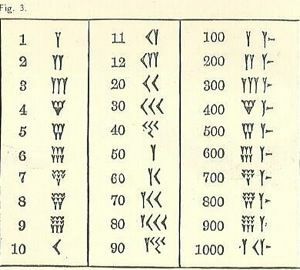
Siden vi vokste opp med et annet system, er babyloniske tall forvirrende.

I det minste løper tallene fra høyt til venstre og lavt til høyre, som vårt arabiske system, men resten vil antagelig virke ukjent. Symbolet for en er en kile eller Y-formet. Dessverre representerer Y også en 50. Det er noen få separate symboler (alle basert på kilen og linjen), men alle andre tall dannes av dem.

Husk at skrivemåten er kileskrift eller kileformet. På grunn av verktøyet som brukes til å tegne linjene, er det en begrenset variasjon. Kilen kan ha eller ikke ha en hale, tegnet ved å trekke den kuleformede skrivpennen langs leiren etter påtrykk av delen trekantform.

De 10, beskrevet som et pilspisser, ser ut som

Tre rader på opptil 3 små 1s (skrevet som Ys med noen forkortede haler) eller 10s (a 10 er skrevet som

Det er tre sett med cuneiform nummer klynger fremhevet i illustrasjonen over.

Akkurat nå er vi ikke opptatt av verdien deres, men med å demonstrere hvordan du vil se (eller skrive) hvor som helst fra 4 til 9 av samme nummer gruppert sammen. Tre går på rad. Hvis det er en fjerde, femte eller sjette, går den under. Hvis det er en syvende, åttende eller niende, trenger du en tredje rad.

De følgende sidene fortsetter med instruksjoner om utførelse av beregninger med den babylonske cuneiformen.

Fra det du har lest over om Soss - som du vil huske er babyloneren i 60 år, kilen og pilspissen - som er beskrivende navn for kuleformete merker, se om du kan finne ut hvordan disse beregningene fungerer. Den ene siden av det streklignende merket er tallet og den andre er firkanten. Prøv det som en gruppe. Hvis du ikke kan finne ut av det, kan du se på neste trinn.

Kan du finne ut av det nå? Gi det en sjanse.

...

Det er 4 klare kolonner på venstre side etterfulgt av et bindestrek-lignende skilt og 3 kolonner på høyre side. Ser vi på venstre side, tilsvarer 1s-kolonnen faktisk de to kolonnene nærmest "bindestrek" (indre kolonner). De to andre, ytre kolonnene telles sammen som 60-talls kolonnen.

• 4-
• 3-Y = 3.
• 40+3=43.
• Det eneste problemet her er at det er et annet nummer etter dem. Dette betyr at de ikke er enheter (stedet). De 43 er ikke 43-ene, men 43-60-tallet, siden det er det sexagesimale (base-60) systemet og det er i Soss som den nedre tabellen indikerer.
• Multipliser 43 med 60 for å få 2580.
• Legg til neste nummer (2-
• Du har nå 2601.
• Det er kvadratet på 51.

Den neste raden har 45 i Soss kolonne, så multipliserer du 45 med 60 (eller 2700), og legger deretter til 4 fra enhetskolonnen, så har du 2704. Kvadratroten av 2704 er 52.

Kan du finne ut hvorfor det siste tallet = 3600 (60 kvadrat)? Tips: Hvorfor er det ikke 3000?